15 Easy viz for multilevel models with `ggeffects`

Author

Josh Gilbert

An awesome convenience function for graphing regression models is the ggeffects package. It is the best equivalent we have found in R to Stata’s margins. We demonstrate with the HSB data.

# load libraries
library(tidyverse)
library(lme4)
library(ggeffects)
library(sjPlot)
library(haven)

# clear memory
rm(list = ls())

# load HSB data
hsb <- read_dta("data/hsb.dta")

To show off ggeffects we first fit some models with 2- and 3-way interactions. Such complex models can be hard to interpret from the coefficients alone (unless you have a lot of practice).

m1 <- lmer(mathach ~ ses + (1|schoolid), hsb)
m2 <- lmer(mathach ~ ses + sector + (1|schoolid), hsb)
m3 <- lmer(mathach ~ ses*sector + (1|schoolid), hsb)
m4 <- lmer(mathach ~ ses*sector*female + (1|schoolid), hsb)

# tabulate results with tab_model
tab_model(m1, m2, m3, m4,
          p.style = "stars",
          show.ci = FALSE,
          show.se = TRUE)

	mathach		mathach		mathach		mathach
Predictors	Estimates	std. Error	Estimates	std. Error	Estimates	std. Error	Estimates	std. Error
(Intercept)	12.66 ^***	0.19	11.72 ^***	0.23	11.80 ^***	0.23	12.41 ^***	0.25
ses	2.39 ^***	0.11	2.37 ^***	0.11	2.95 ^***	0.14	2.73 ^***	0.19
sector			2.10 ^***	0.34	2.14 ^***	0.34	2.16 ^***	0.38
ses × sector					-1.31 ^***	0.21	-1.26 ^***	0.30
female							-1.16 ^***	0.21
ses × female							0.34	0.26
sector × female							-0.05	0.35
(ses × sector) × female							-0.05	0.40
Random Effects
σ²	37.03		37.04		36.84		36.63
τ₀₀	4.77 _schoolid		3.69 _schoolid		3.69 _schoolid		3.40 _schoolid
ICC	0.11		0.09		0.09		0.09
N	160 _schoolid		160 _schoolid		160 _schoolid		160 _schoolid
Observations	7185		7185		7185		7185
Marginal R² / Conditional R²	0.077 / 0.182		0.114 / 0.195		0.118 / 0.199		0.127 / 0.202
* p<0.05 p<0.01 * p<0.001

15.1 Graph the Results with `ggeffects`

If we just call ggeffect on the model object, we get a bunch of predicted values:

ggeffect(m1)

$ses
# Predicted values of mathach

ses | Predicted |       95% CI
------------------------------
 -4 |      3.10 |  2.19,  4.00
 -3 |      5.49 |  4.77,  6.21
 -2 |      7.88 |  7.32,  8.43
 -1 |     10.27 |  9.85, 10.69
  0 |     12.66 | 12.29, 13.03
  1 |     15.05 | 14.62, 15.47
  2 |     17.44 | 16.88, 17.99
  3 |     19.83 | 19.10, 20.55


attr(,"class")
[1] "ggalleffects" "list"        
attr(,"model.name")
[1] "m1"

We can pipe that into plot to get a nice plot:

ggeffect(m1) |> 
  plot()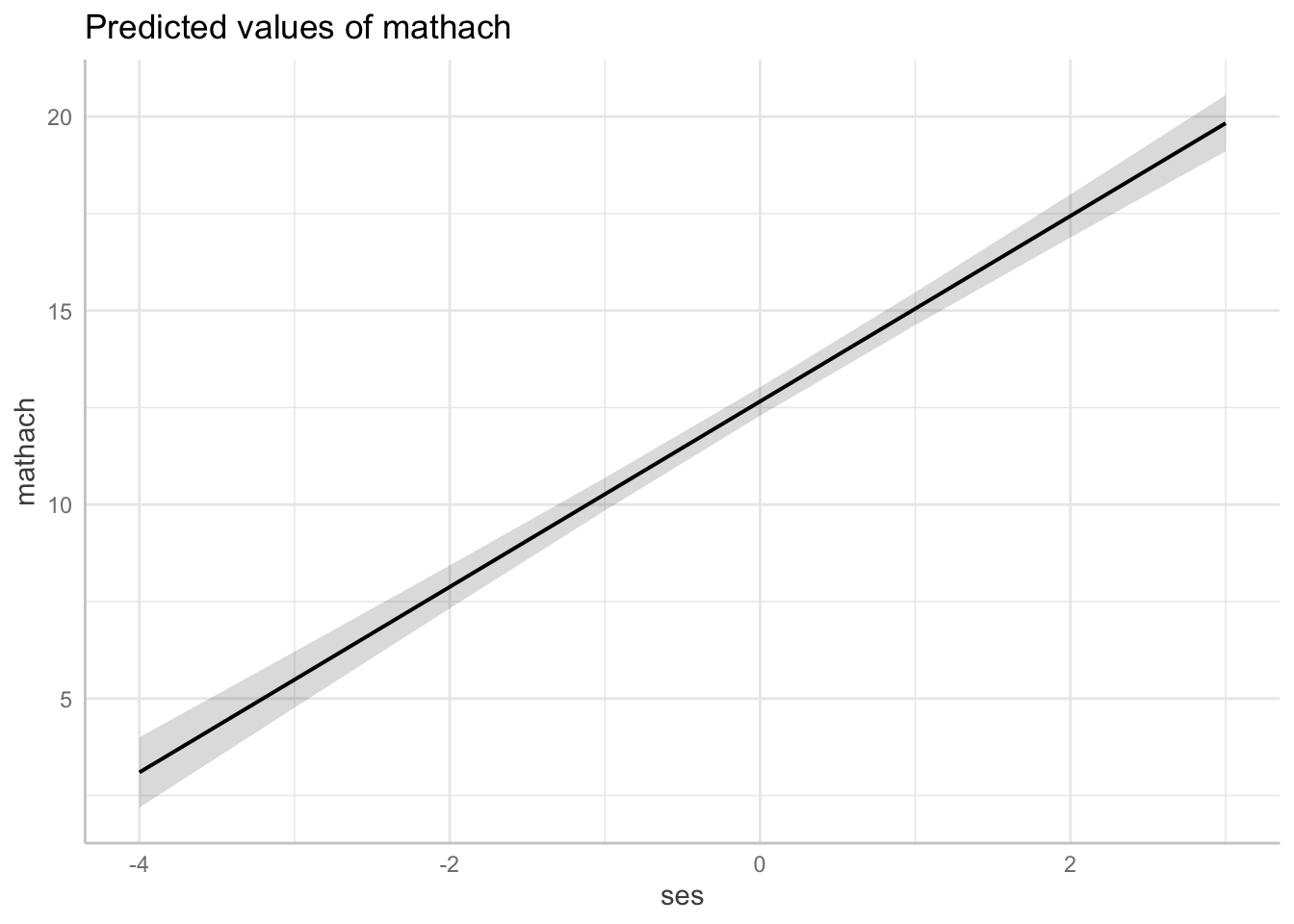

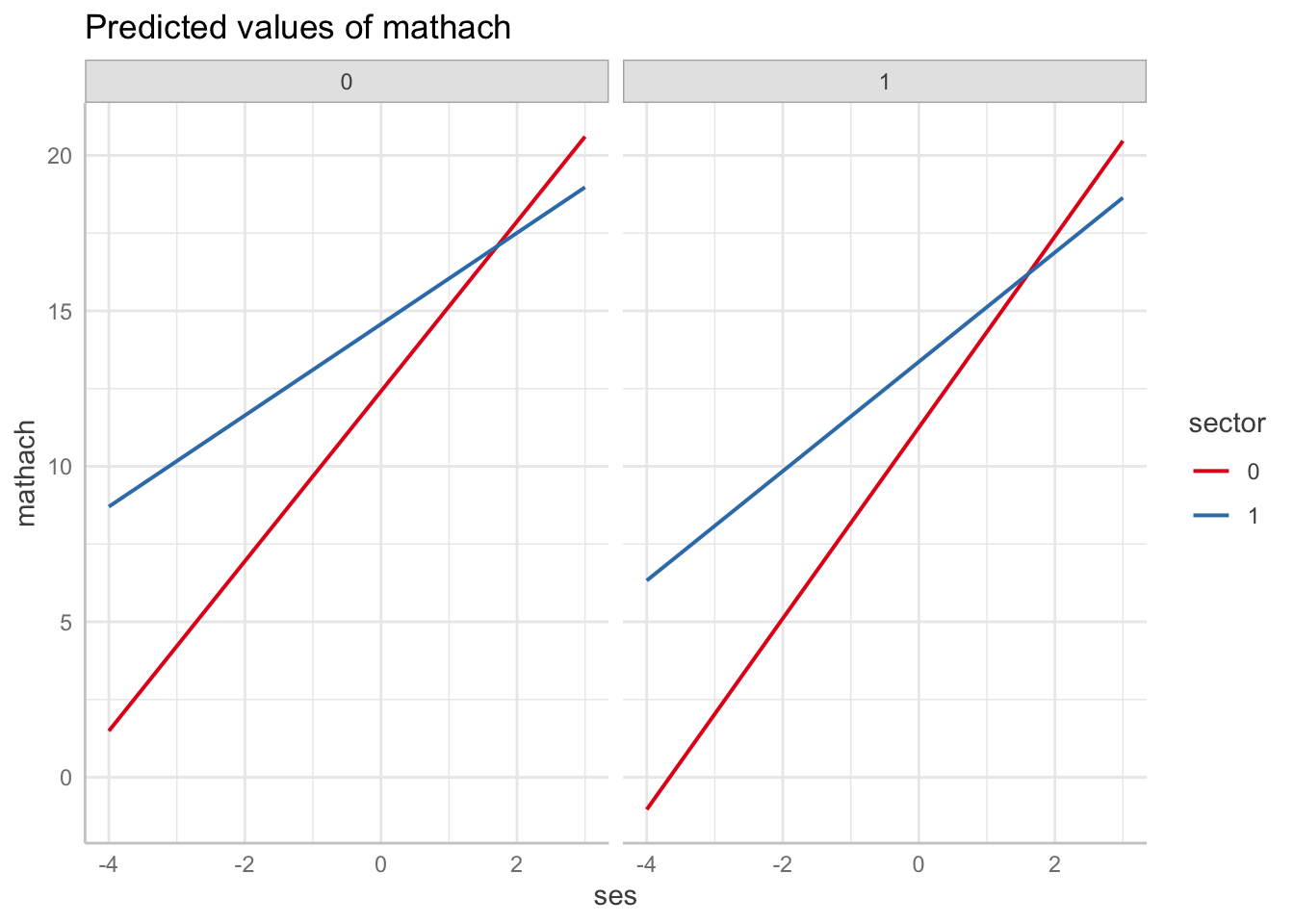
With multiple covariates, we can use the terms argument, which allows us to aggregate our data within different groups. The first term will be our \(x\)-axis, the second will get mapped to color, the third to facet. This makes visualizing our interactions super easy! Any covariates included in the model but not included in terms are held constant at their means.

ggeffect(m2, terms = c("ses", "sector")) |> 
  plot(ci = FALSE, add.data = TRUE)

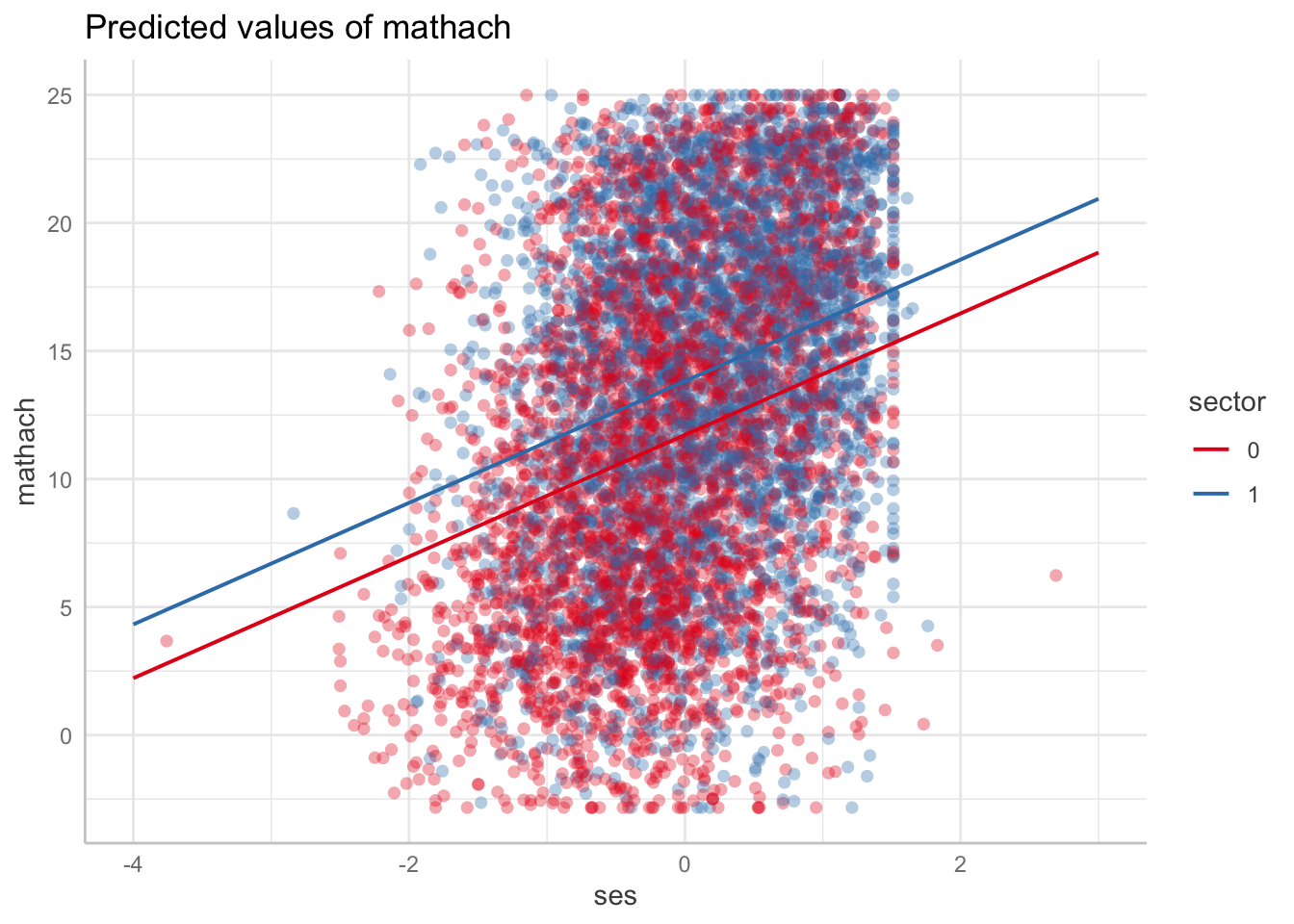
ggeffect(m3, terms = c("ses", "sector")) |> 
  plot(ci = FALSE)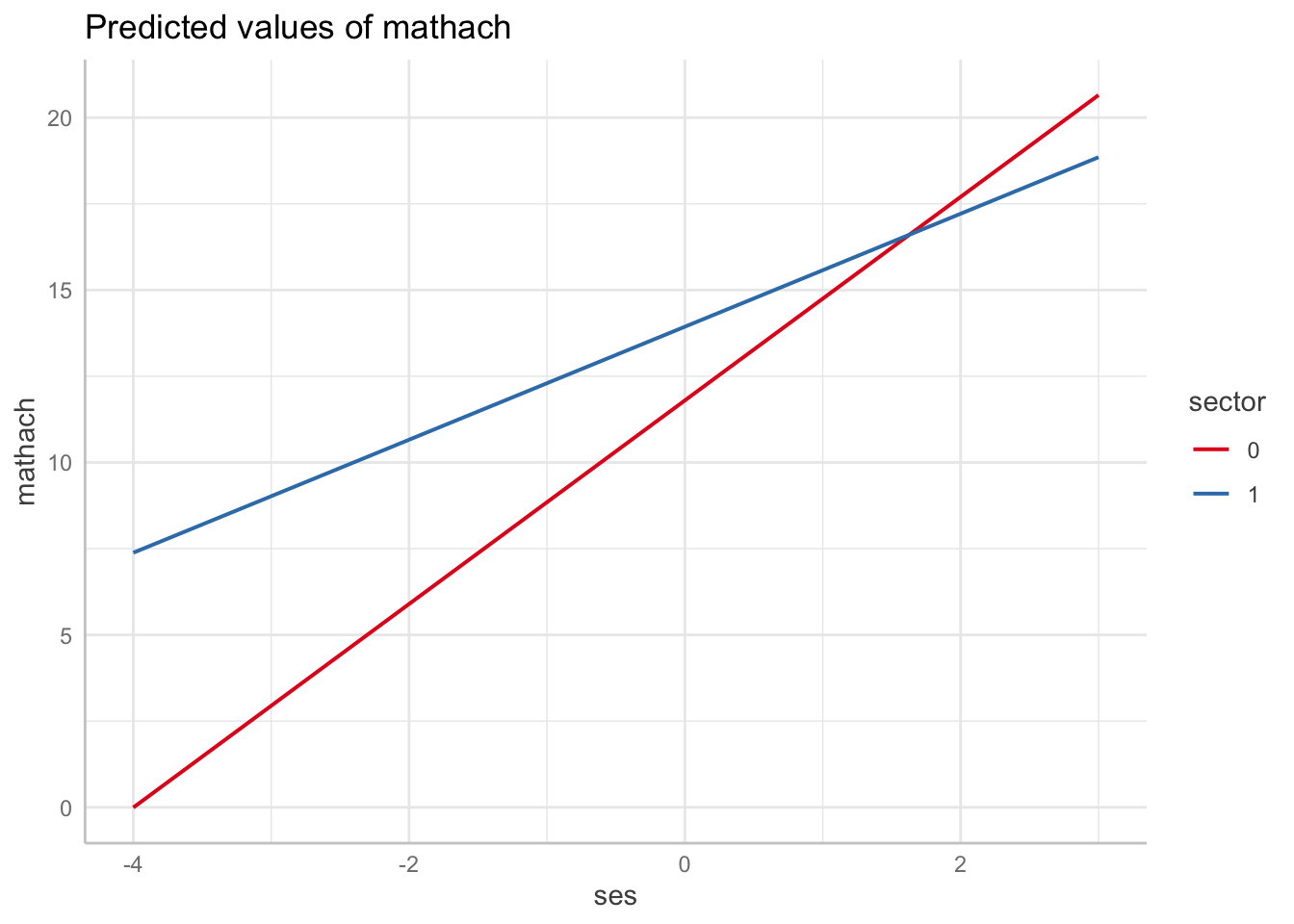

ggeffect(m4, terms = c("ses", "sector", "female")) |> 
  plot(ci = FALSE)

15.1 Graph the Results with ggeffects

15.1 Graph the Results with `ggeffects`